Tingkat Pengaruh dengan R Kuadrat
Melalui kelas ini, kamu diajak untuk:
- Mengenal konsep, karakteristik, dan nilai-nilai umum dari R2.
- Mengidentifikasi komponen-komponen rumus untuk mencari R2.
Pengantar
Di kelas pengantar statistik, kita telah diajak untuk mengenal R untuk mencari korelasi koefisien. Semakin jauh R dari 0, berarti ada korelasi antara variabel satu dengan lainnya. Sebaliknya, jika R = 0 berarti tidak ada korelasi antar variabel. Dalam regresi, kita akan beranjak dari R menuju R2.
Tentang R2
R2 adalah cara yang kita gunakan untuk menghitung pengaruh variabel independen terhadap variabel dependen. Semakin jauh R2 dari angka 0, semakin tinggi pengaruh variabel independen terhadap variabel dependen. Namun, berbeda dengan R, R2 tidak mengenal angka negatif. Sederhananya, karena tingkat korelasi dipangkatkan, maka R2 tidak akan memunculkan angka kurang dari 0. Dengan kata lain, tingkat R2 hanya berkisar dari 0 sampai 1.
Pertanyaannya, di tingkat mana R2 dapat dikatakan berpengaruh?
Seperti ambang batas p-value yang umum menggunakan 0.05, tidak ada ambang batas pasti untuk R2. Para peneliti justru mengemukakan bahwa area studi yang berbeda memiliki kisaran R2 yang berbeda pula.
Ketuk untuk melihat lebih jauh.
Sains Murni
Dalam studi sains murni, tingkat R2 cenderung diterima ketika nilai berada di angka 0.60 atau lebih.
Marketing
Studi-studi marketing secara umum membagi nilai R2 menjadi 3. 0.25-0.50 (lemah), 0.51- 0.75 (moderat), dan 0.76 ke atas (kuat).
Sosial & Budaya
Studi-studi sosial dan budaya cenderung masih menerima tingkat R2 kisaran > 0.10.
Mencari Pengaruh dengan R2
Sekarang saatnya menuju bagian paling penting, yaitu menghitung R2. Rumus mencari R2 adalah sebagai berikut.
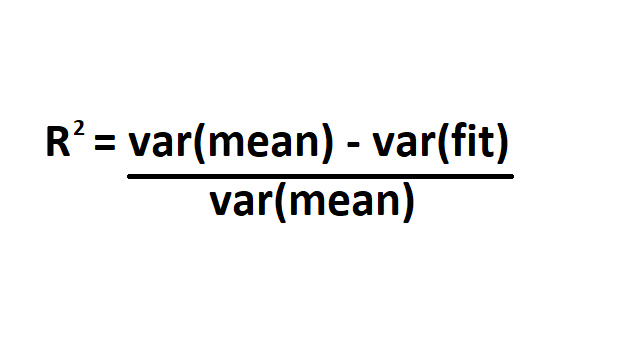
Keterangan:
- var(mean) = varians di sekitar mean
- var(fit) = varians di sekitar fit atau garis
Var(mean) juga bisa disebut sebagai SST (Sum of Squared Total). Artinya sama, yaitu kuadrat selisih antara variabel dependen yang diamati dan rata-ratanya. Var(fit) juga bisa disebut SSE (Sum of Squared Error) atau Residual Sum of Squares (RSS).
Misal ditemukan bahwa R2 = 0.8 atau 80%. Hasil ini bagus, 80% varians dari variabel dependen dijelaskan oleh variabel independen. Jika hasil R2 = 0.07, berarti variabel independen hanya menyumbang 7% dari varians variabel dependen.
Di kasus kali ini, kita akan menggunakan kembali data berat badan atlet dan kecepatan lari di materi sebelumnya. Sekarang, mari lihat demonstrasi penghitungan R2 dengan Python di bawah ini.
# Memunculkan summary
X2 = sm.add_constant(X)
est = sm.OLS(y, X2)
est2 = est.fit()
print(est2.summary())
Python kemudian memunculkan hasil seperti ini.
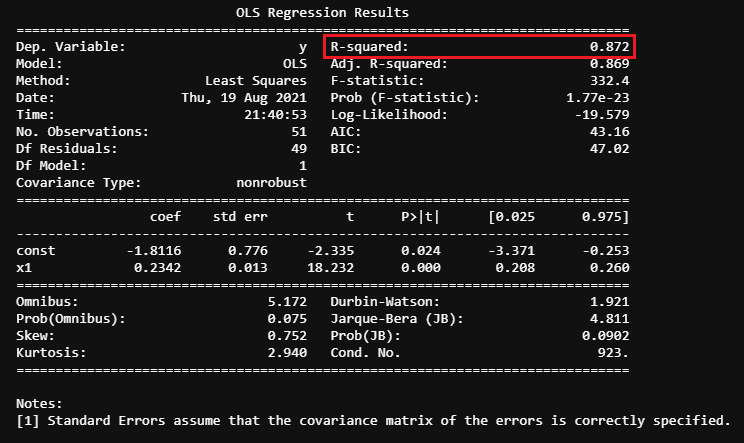
Dari hasil di atas, dapat dilihat bahwa R2 = 0.872 atau 87,2%. Dengan demikian, dapat dikatakan bahwa sebesar 87,2% varian dari variabel dependen dijelaskan oleh variabel independen.
Pro Tips
- Semakin dekat nilai R2 dengan angka 1, semakin tinggi pengaruh variabel independen terhadap variabel dependen.
- Untuk mencari R2, kita perlu menemukan: 1) kuadrat selisih antara variabel dependen yang diamati serta rata-ratanya, dan 2) jumlah residual kuadrat.
Kuis
Apa yang membedakan R2 dengan R?