P-Value Regresi
Melalui kelas ini, kamu diajak untuk:
- Mengenal konsep p-value untuk mengukur signifikansi pengujian regresi.
- Memahami cara menginterpretasikan hasil p-value dalam ringkasan hasil pengujian regresi.
Pengantar
Kita telah mengulas R2 untuk mencari tingkat korelasi dan pengaruh variabel independen terhadap variabel dependen. Misal dalam perhitungan yang kita lakukan, kita mendapatkan angka 0.8 yang berarti 80% variasi dari variabel dependen dapat dijelaskan oleh variabel independen. Kita bisa saja puas dengan perhitungan kita. Namun, ada satu langkah lagi yang dapat kita lakukan untuk memastikan perhitungan kita signifikan secara statistik, yaitu mencari p-value.
Contoh Kasus
Pertama-tama, mari kita lihat ilustrasi kasus di bawah ini.
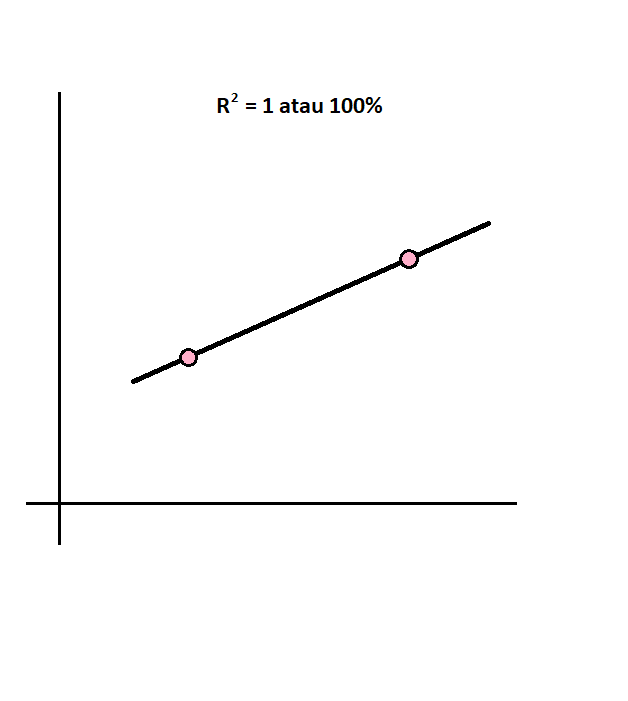
Dari contoh visualisasi di atas, ditemukan bahwa R2 = 1. Berarti, ada 100% pengaruh variabel independen terhadap variabel dependen. Namun titik data yang divisualisasikan hanya 2.
Pertanyaan yang kemudian muncul adalah, apakah data ini dapat merepresentasikan populasi? Pertanyaan lebih lanjut adalah, dengan pertimbangan sampel dan populasi, apakah hasil R2 dapat dikatakan signifikan secara statistik?
Lagi-lagi P-Value
Untuk menjawab dua pertanyaan di bagian sebelumnya, lagi-lagi kita harus kembali membahas p-value. P-value adalah probabilitas kebenaran dari hipotesis nol. Semakin tinggi nilai p-value, semakin besar kemungkinan hipotesis nol adalah benar. Dengan kata lain, untuk menolak hipotesis nol, kita membutuhkan p-value yang kecil. Ambang batas p-value yang umum digunakan adalah 0.05 atau 5% probabilitas kebenaran dari hipotesis nol.
Misal kita mendapatkan R2 = 0.9 atau 90%, namun p-value adalah 0.8 (lebih dari 0.05). Meskipun R2 bisa dibilang menjelaskan bahwa ada korelasi antara variabel dependen dengan variabel independen, namun hasil tersebut bisa dikatakan tidak signifikan secara statistik. Dalam artian, ada masalah dengan data sampel yang tidak akan menghasilkan tingkat korelasi yang sama jika ditarik luas ke populasi, seperti kasus di bagian sebelumnya.
Mencari P-Value
Sekarang, saatnya kita mencari p-value dari contoh kasus materi sebelumnya, yaitu pengaruh berat badan atlet terhadap kecepatan lari mereka. Lihat susunan kode Python di bawah ini.
# Memunculkan summary
X2 = sm.add_constant(X)
est = sm.OLS(y, X2)
est2 = est.fit()
print(est2.summary())
Hasil dari Python:
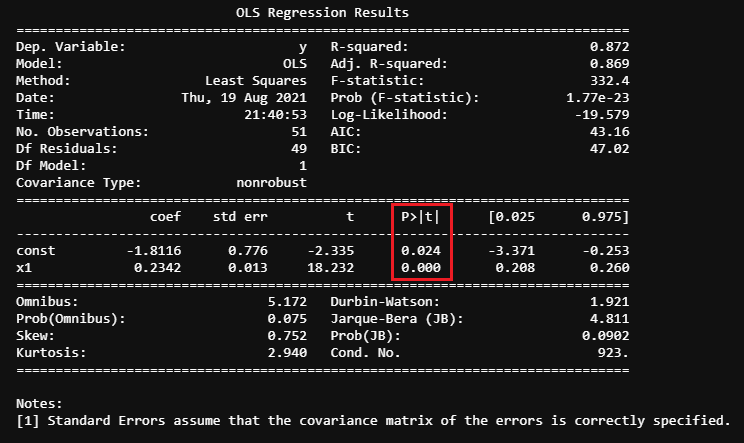
Dari hasil di atas, dapat dilihat bahwa p-value konstanta dan x1 lebih kecil dari ambang batas (0.05). Dengan demikian, dapat dikatakan bahwa pengujian ini signifikan secara statistik dan kita dapat menolak hipotesis nol.
Pro Tips
- Setelah menghitung R2, kita perlu memastikan bahwa probabilitas kebenaran adanya korelasi dan pengaruh antar variabel signifikan secara statistik.
- Untuk mengukur signifikansi pengujian regresi, kita perlu mencari p-value. Jika p-value lebih kecil dari ambang batas (umumnya 0.05), maka pengujian kita dapat menolak hipotesis nol.
Kuis
Apa konsekuensi dari p-value yang besar dalam pengujian regresi?