Mencari Kemiringan Garis
Melalui kelas ini, kamu diajak untuk:
- Memahami konsep line of best fit untuk menentukan kemiringan garis dalam menjelaskan tren data.
- Mengenal least square, metode untuk mencari line of best fit.
Pengantar
Kita telah diajak mengenal konsep-konsep mendasar mengenai regresi. Sekarang, saatnya kita beranjak ke bagian paling seru, yaitu hitung-menghitung. Di materi ini, kita akan mengulas line of best fit, konsep yang amat penting dalam perhitungan regresi linear.
Mengenal Line of Best Fit
Dalam menghitung regresi linear, mula-mula kita perlu berkenalan dengan line of best fit. Line of best fit adalah garis yang paling sesuai dengan persebaran data. Garis ini digunakan untuk melihat kecenderungan tren dari data.
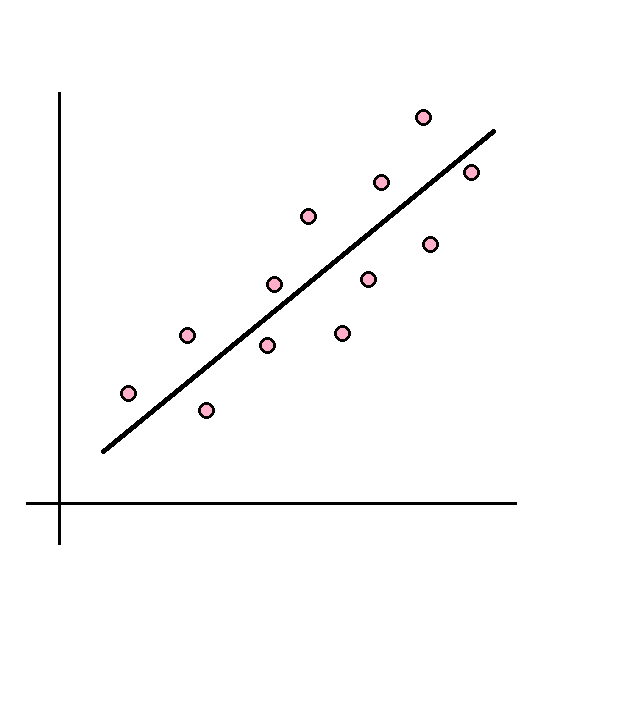
Untuk memahami line of best fit, pahami terlebih dahulu istilah-istilah yang relevan.
Ketuk untuk memahami lebih jauh.
Garis
Garis yang menggambarkan kecenderungan tren dan korelasi data.
Titik Data
Hasil data sampel yang tersebar dalam grafik, direpresentasikan dengan titik.
Residual
Jarak antara masing-masing titik data dengan garis.
Menerka-nerka Garis Data yang Sesuai
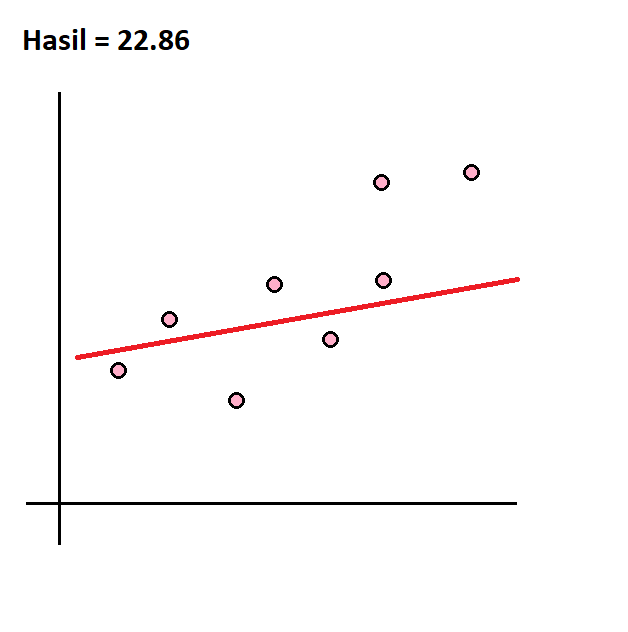
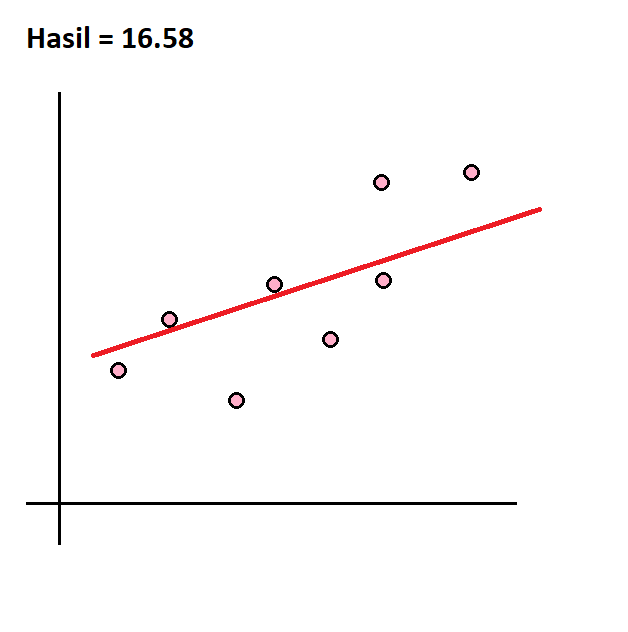
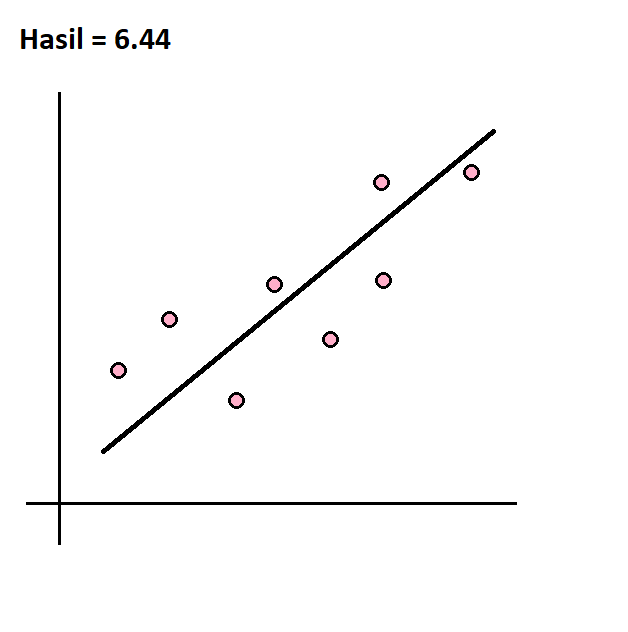
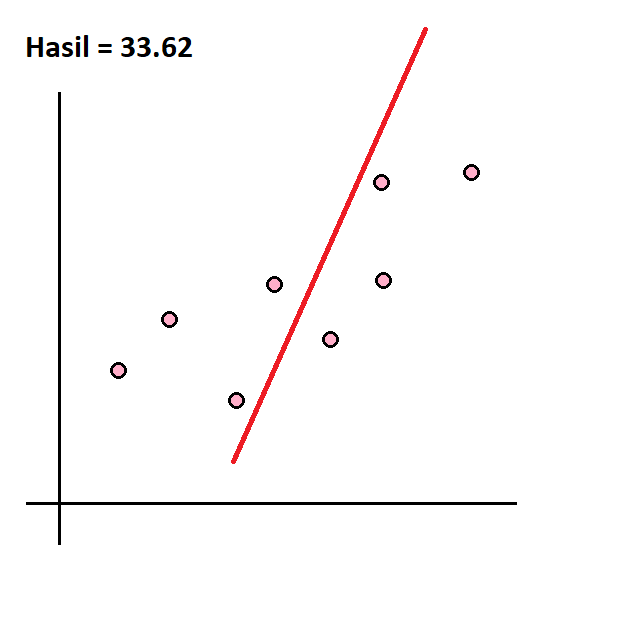
Garis data yang sesuai dihitung berdasarkan angka residual paling kecil. Dalam artian, semakin dekat jarak masing-masing titik data terhadap garis, semakin sesuai garis untuk menjelaskan tren. Untuk mengetahui jarak antara garis dan titik data, kita menggunakan SUM (penjumlahan) dari residual yang dipangkatkan. Semakin mendekati nol, semakin sesuai garis dengan titik-titik data.
Kita bisa saja mengira garis data yang sesuai dengan menggambar garis secara acak untuk menjelaskan persebaran data.
Geser untuk melihat contoh-contohnya.
Percobaan 1
Di percobaan pertama, hasil masih amat jauh dengan angka 0. Dengan kata lain, garis ini tidak cocok untuk menjelaskan data.
Percobaan 2
Kita memutar sedikit garis di percobaan 2. Hasilnya lebih kecil dari percobaan 1, namun masih jauh dari angka 0.
Percobaan 3
Di percobaan 3 kita kembali memutar sedikit garis. Angka ini lebih dekat dengan 0 ketimbang percobaan-percobaan sebelumnya.
Percobaan 4
Hati-hati memutar garis terlalu ekstrem, bisa jadi angkanya justru melonjak naik, alih-alih semakin mendekati 0.
Menggunakan Least Square
Lalu bagaimana caranya mencapai angka 0 agar kita mampu mendapatkan garis ideal? Kali ini, kita diajak untuk mengenal metode least square. Seperti namanya, kita akan mencari hasil pangkat terkecil. Rumusnya adalah y = a + bX. y adalah variabel dependen, a adalah konstanta, b adalah kemiringan garis, dan X adalah variabel independen.
Kita dapat mencari y dan kemiringan garis yang sesuai dengan persebaran data dengan kalkulator atau bahasa pemrograman tertentu. Di materi ini, kita akan menggunakan Python.
Kali ini, kita akan diajak untuk melihat korelasi antara berat badan atlet dengan kecepatan lari. Berat badan atlet kita pasang sebagai variabel independen (X) dan kecepatan lari adalah variabel dependen (y). Lihat susunan kode di bawah ini.
# memasukkan data
data = pd.read_csv("regresi_sederhana.csv")
# variabel independen
X = data["Berat Badan"].values.reshape(-1,1)
# variabel dependen
y = data["Kecepatan Lari"].values.reshape(-1,1)
# mengaktifkan function regresi linear
reg = LinearRegression()
reg.fit(X, y)
# memunculkan hasil y = ax + b
print("Model Linear: Kecepatan Lari = {:.5} + {:.5} *
Berat Badan".format(reg.intercept_[0], reg.coef_[0][0]))
# mengatur visualisasi
predictions = reg.predict(X)
plt.figure(figsize=(10, 5))
plt.scatter(
data["Berat Badan"],
data["Kecepatan Lari"],
c='black'
)
plt.plot(
data["Berat Badan"],
predictions,
c='blue',
linewidth=2
)
plt.xlabel("Berat Badan (kg)")
plt.ylabel("Kecepatan Lari (detik)")
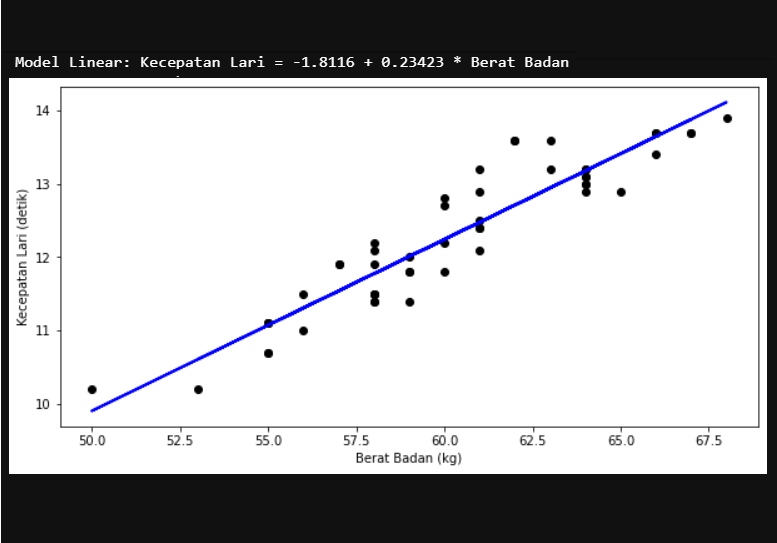
plt.show()Dari susunan kode di atas, didapatkan hasil dan visualisasi seperti ini.
Pro Tips
- Line of best fit adalah penyesuaian kemiringan garis untuk menjelaskan tren dari persebaran data.
- Dalam mencari line of best fit, kita perlu mengenal residual atau jarak antara setiap titik data dengan garis tren.
- Least square adalah cara paling mudah untuk mencari kemiringan garis dengan rumus y = ab + x.
Kuis
Apa keterangan komponen X dalam rumus y = a + bX untuk mencari least square?