Perbedaan
Materi ini akan mengajarkan soal:
- Mengidentifikasi jenis pengujian signifikansi perbedaan berdasarkan tipe variabel.
- Mengetahui cara membaca hasil dan p-value masing-masing pengujian.
Pengantar
Penyedia layanan bimbingan belajar A memiliki hipotesis bahwa ada perbedaan hasil ujian yang signifikan antara siswa SMA di Yogyakarta yang mengikuti bimbingannya dengan yang tidak. Mereka mengambil sampel dan menemukan bahwa rata-rata nilai siswa yang dibimbingnya adalah 87,5, sementara rata-rata siswa yang tidak dibimbingnya adalah 75.
Mereka bisa saja berhenti pada hasil rata-rata dari dua grup di atas. Namun, saat mengambil data, mereka menggunakan sampel. Rata-rata dari sampel belum tentu bisa merepresentasikan seluruh populasi. Maka dari itu, mereka perlu melakukan pengujian lebih lanjut, yang dalam kasus mereka, menggunakan t-test.
Jenis Pengujian Hipotesis
Di materi sebelumnya, kita telah mengenal jenis-jenis pengujian hipotesis untuk mengukur signifikansi perbedaan, seperti t-test dan ANOVA. Kali ini, kita akan mengulas jenis-jenis pengujian hipotesis yang umum digunakan berdasarkan tipe variabel, kategori dan numerik.

Sebagai disclaimer, materi ini akan menggunakan bahasa pemrograman Python untuk mengaplikasikan pengujian. Ada banyak software untuk menguji hipotesis, mulai dari SAS, R, Python, dan kalkulator-kalkulator daring yang dapat kita akses.
Satu Variabel Kategori (Dua Level) dan Satu Variabel Numerik
Mari kembali ke ilustrasi penyedia bimbingan belajar A. Setelah mendapat data rata-rata nilai dari dua grup berbeda berdasarkan sampel, mereka melakukan testing menggunakan t-test.
T-test adalah jenis testing yang kita gunakan ketika kita ingin melihat perbedaan antara satu variabel kategori dengan dua level (siswa yang ikut bimbingan dan siswa yang tidak ikut bimbingan) dengan satu variabel numerik (nilai ujian). Rumus dari t-test pada kasus ini adalah sebagai berikut:
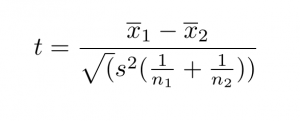
Keterangan:
t = nilai t
x1 and x2 = mean dari dua grup yang dibandingkan
n1 and n2 = ukuran sampel
S2 = estimator varians umum dari dua sampel
Mereka menggunakan Python untuk menerapkan t-test dengan dua sampel data. Mereka kemudian mendapatkan hasil sebagai berikut:
[in]:
# Kelompok pertama (mengikuti bimbingan)
data1 = [88, 85, 89, 92, 94, 90, 85, 82, 80, 91, 90, 84, 83, 88, 92]
# Kelompok kedua (tidak mengikuti bimbingan)
data2 = [70, 72, 75, 75, 77, 80, 74, 75, 82, 73, 75, 75, 78, 78, 77]
# menerapkan t-test
stat, p = ttest_ind(data1, data2)
# perintah memunculkan hasil
print('stat = %.3f, p = %.10f' % (stat, p))
# perintah menjelaskan hasil
if p < 0.05:
print("Berhasil menolak hipotesis nol.")
else:
print("Gagal menolak hipotesis nol.")
[out]:
stat = 8.858, p = 0.0000000013
Berhasil menolak hipotesis nol.Dari hasil di atas, dapat kita lihat bahwa p-value < 0.05. Maka, hipotesis nol berhasil ditolak. Dengan kata lain, ada perbedaan signifikan antara siswa yang mengikuti bimbingan dan yang tidak.
Satu Variabel Kategori (Lebih dari Dua Level) dan Satu Variabel Numerik
Perusahaan media memiliki hipotesis bahwa ada perbedaan signifikan antara pembaca berdasarkan tiga kategori generasi (Gen Z, Millennial, dan Baby Boomer) dan tingkat ketertarikan mereka membaca konten berita politik. Dari hipotesis tersebut, dapat dilihat bahwa ada satu variabel kategori dengan tiga level (Gen Z, Millennial, dan Baby Boomer) dan satu kategori numerik (tingkat ketertarikan membaca berita politik).
Untuk hipotesis dengan variabel-variabel seperti di atas, mereka menggunakan jenis tes ANOVA satu arah. Kita menggunakan ANOVA satu arah untuk menguji satu variabel kategori dengan lebih dari dua level dan satu variabel numerik. Lihat rumus ANOVA satu arah di bawah ini:
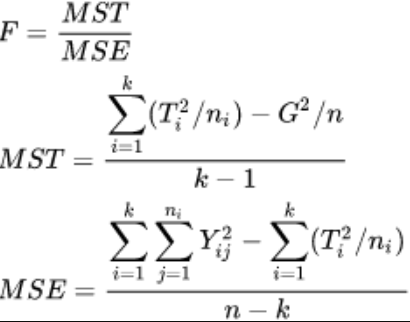
Keterangan:
F = rasio varians untuk tes keseluruhan
MST = kuadrat rata-rata karena perlakuan/kelompok (antar kelompok)
MSE = kuadrat rata-rata karena error (dalam kelompok, kuadrat rata-rata residual)
Yij = pengamatan
Ti = total grup
G = total keseluruhan dari semua pengamatan
ni = jumlah dalam grup i
n = jumlah total pengamatan.
Mereka kemudian menggunakan software Python untuk menerapkan tes ANOVA satu arah. Setelah itu, mereka mendapatkan hasil sebagai berikut:
[in]:
# membaca data tabel Excel yang dijadikan CSV
data = pd.read_csv("anova.csv")
# menerapkan tes ANOVA satu arah atau F
stat, p = f_oneway(data["Gen Z"], data["Millennial"], data["Baby Boomer"])
# perintah untuk memunculkan hasil
print('F = %.3f, p-value = %.3f' % (stat, p))
# perintah untuk menjelaskan hasil
if p < 0.05:
print("Berhasil menolak hipotesis nol.")
else:
print("Gagal menolak hipotesis nol.")
[out]:
F = 1.697, p-value = 0.193
Gagal menolak hipotesis nol.Dari hasil di atas, dapat dilihat bahwa p-value > 0.05. Maka, hasil tes gagal menolak hipotesis nol. Dengan kata lain, tidak ada perbedaan signifikan antara kategori generasi dengan tingkat ketertarikan membaca berita politik.
Lebih dari Satu Variabel Kategori (Dua Level atau Lebih) dan Satu Variabel Numerik
Sebuah lembaga riset memiliki hipotesis bahwa ada perbedaan yang signifikan antara rata-rata pendapatan per bulan laki-laki dan perempuan. Namun, mereka menambah satu variabel lain, yakni tempat tinggal (pedesaan dan perkotaan). Dari sampel yang mereka ambil, mean dari setiap grup adalah sebagai berikut:
- Laki-laki perkotaan Rp 4.696.656
- Perempuan perkotaan Rp 3.762.381
- Laki-laki pedesaan Rp 2.613.067
- Perempuan pedesaan Rp 1.727.564
Dari hipotesis yang mereka ajukan, dapat dilihat bahwa terdapat dua variabel kategori (gender dan tempat tinggal) dengan masing-masing dua level (laki-laki dan perempuan, perkotaan dan pedesaan) dan satu variabel numerik (rata-rata pendapatan). Maka, jenis tes yang mereka gunakan adalah ANOVA dua arah. Lihat rumusnya di bawah ini:
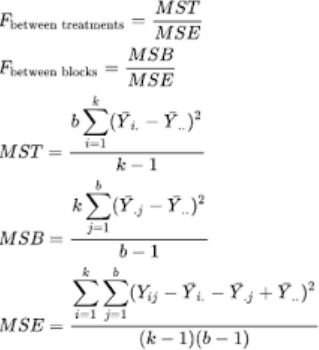
Keterangan:
F = rasio varians untuk uji kesetaraan perlakuan dan rata-rata blok
MST = kuadrat rata-rata karena perlakuan/kelompok (antar kelompok)
MSB = kuadrat rata-rata karena blok (antar blok)
MSE = kuadrat rata-rata karena error (dalam grup, residual mean square)
Yij = observasi
Y bar i. = mean dari kelompok treatment
Y bar .j = mean dari blok
Y bar .. = mean dari besar dari semua pengamatan.
Dari rumus di atas, dapat dilihat bahwa hasil yang kita cari adalah signifikansi perbedaan berdasarkan treatment/kelompok dan blok. Setelah menerapkan tes ANOVA dua arah, mereka mendapatkan hasil sebagai berikut:
- Factor A = 7130.4541
- P-value Factor A = 0.007539
- Factor B = 1392.181
- P-Value Factor B = 0.01706
Dari hasil di atas, dapat dilihat bahwa p-value dari faktor pertama (gender) dan kedua (tempat tinggal) < 0.05. Maka, kedua hasil tersebut menolak hipotesis nol. Dengan kata lain, ada perbedaan signifikan antara gender dan tempat tinggal dengan rata-rata pendapatan per bulan.
Pro Tips
- Ketika kita ingin melihat signifikansi perbedaan antara satu variabel kategori (dua level) dengan satu variabel numerik, kita dapat menggunakan t-test.
- Signifikansi perbedaan antara satu variabel kategori (lebih dari dua level) dengan satu variabel numerik menggunakan tes ANOVA satu arah.
- Jika kita ingin melihat signifikansi perbedaan antara lebih dari satu variabel kategori (dua level atau lebih) dengan satu variabel numerik, kita bisa memakai tes ANOVA dua arah.
Kuis
Sebuah perusahaan sepatu memiliki hipotesis bahwa ada perbedaan kecepatan lari dengan jarak 100 meter antara atlet yang menggunakan sepatunya dengan yang tidak. Apa jenis pengujian yang dapat digunakan perusahaan tersebut?