Korelasi

Materi ini akan mengajarkan soal:

• Mengidentifikasi jenis pengujian signifikansi korelasi berdasarkan tipe variabel.
• Mengetahui cara membaca hasil dan p-value masing-masing pengujian.

Jenis-jenis Pengujian Korelasi

Di materi ini, kita diajak untuk mengenal jenis testing berdasarkan tipe variabel. Ada dua jenis pengujian yang akan kita ulas, menguji korelasi antara dua variabel kategori dan korelasi antara dua variabel numerik.

Sama seperti materi sebelumnya, materi ini akan menggunakan bahasa pemrograman Python untuk mengaplikasikan pengujian.

Dua Variabel Kategori

Sebuah lembaga riset kesehatan memiliki data jumlah masyarakat perokok dan non-perokok berdasarkan gender. Mereka memiliki hipotesis bahwa ada korelasi yang cukup signifikan antara gender dengan perilaku merokok. Gender dan perilaku merokok adalah variabel kategori. Maka, mereka melakukan tes chi-square. Lihat rumusnya di bawah ini:

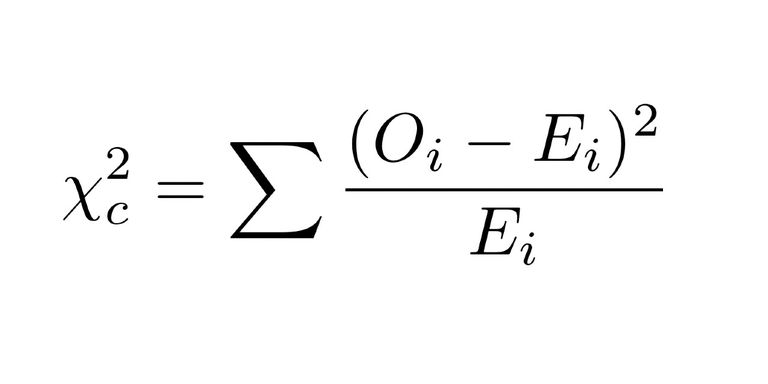
Keterangan:
c = derajat kebebasan
E = nilai yang diamati
O = nilai yang diekspektasikan

Dari data yang mereka miliki, berikut perilaku merokok masyarakat berdasarkan gender. Persentase perempuan merokok 56 dan tidak merokok sejumlah 144. Kemudian laki-laki sebanyak 88 yang merokok, dan 144 yang tidak merokok. Mereka menggunakan software Python untuk menerapkan tes chi-square. Kemudian, mereka mendapatkan hasil sebagai berikut:

[in]:

# memasukkan data ke dalam tabel 
data = [[56, 144],[88, 112]]
# menerapkan chi-square
stat, p, dof, expected = chi2_contingency(data)
# memunculkan hasil
print('stat = %.3f, p = %.3f' % (stat, p))
# menjelaskan hasil
if p > 0.05:
    print('Tidak memiliki korelasi.')
else:
    print('Memiliki korelasi.')

[out]:

stat = 10.428, p = 0.001
Memiliki korelasi.

Dari hasil di atas, dapat dilihat bahwa p-value dari dua variabel kategori (gender dan perilaku merokok) < 0.05. Maka, kedua hasil tersebut menolak hipotesis nol. Dengan kata lain, ada korelasi antara gender dan perilaku merokok.

Dua Variabel Numerik

Untuk menguji hipotesis mengenai korelasi dua variabel numerik, kita perlu mengenal tes korelasi koefisien yang digagas oleh Pearson. Ada tiga hasil yang mungkin didapatkan, korelasi positif, korelasi negatif, dan tidak ada korelasi.

Ketuk untuk melihat perbedaan ketiga kemungkinan hasil.

Sebagai contoh kasus, sebuah lembaga riset ingin meneliti tentang berat badan atlet lari. Mereka memiliki hipotesis bahwa ada korelasi yang signifikan antara berat badan dan kecepatan lari para atlet. Lembaga riset ini kemudian mengambil sampel dan mengambil data-data berat badan dan kecepatan lari.

Untuk menguji hipotesisnya, mereka menggunakan korelasi koefisien, atau r milik Pearson. Lihat rumusnya di bawah ini:

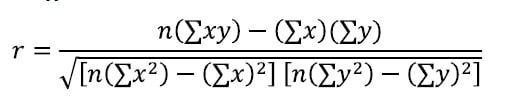
Keterangan:
r = hasil tes
x = variabel 1
y = variabel 2
n = jumlah sampel

Setelah menerapkan tes korelasi menggunakan Python, berikut hasil yang mereka dapatkan:

[in]:

# memasukkan data
data_kg = [65, 60, 62, 58, 61, 55, 67, 57, 58, 60, 55, 64, 66, 59, 63]
data_s = [12.9, 11.8, 13.6, 11.1, 14.2, 11.7, 12.7, 11.9, 11.5, 12.2, 11.3, 12.5, 13.1, 11.9, 13.1]
# menerapkan korelasi koefisien 
stat, p = pearsonr(data_kg, data_s)
# memunculkan hasil
print('stat = %.3f, p = %.3f' % (stat, p))
# menjelaskan hasil
if p > 0.05:
    print('Tidak memiliki korelasi')
else:
    print('Memiliki korelasi')

[out]:

stat = 0.661, p = 0.007
Memiliki korelasi

Dari hasil di atas, dapat dilihat bahwa p-value dari dua variabel numerik (berat badan dan kecepatan lari) < 0.05. Maka, kedua hasil tersebut menolak hipotesis nol. Dengan kata lain, ada korelasi antara berat badan dan kecepatan lari.

Data di atas juga menunjukkan hasil statistik 0,661. Dengan demikian, hasil korelasi yang dimiliki kedua variabel adalah korelasi positif. Kesimpulan dari hasil ini adalah angka berat badan yang lebih tinggi memiliki korelasi dengan waktu kecepatan yang lebih tinggi pula.

Korelasi =/= Pengaruh

Mencari korelasi seringkali disalahartikan sebagai pengaruh. Korelasi koefisien tidak dapat menjelaskan pengaruh karena ia tidak mampu membedakan antara variabel independen dan variabel dependen. Misal pada kasus berat badan dan kecepatan lari, korelasi koefisien tidak bisa menjelaskan apakah kecepatan lari dipengaruhi oleh berat badan atau sebaliknya.

Untuk menguji pengaruh, kita perlu menetapkan variabel independen dan dependen. Misal kita ingin menguji pengaruh berat badan terhadap kecepatan lari, maka kita perlu memperlakukan berat badan sebagai variabel independen dan kecepatan lari sebagai variabel dependen. Model pengujian yang digunakan juga bukan korelasi koefisien, melainkan regresi.

Mengenal Regresi

Regresi adalah metode statistika yang digunakan untuk menguji pengaruh variabel independen terhadap variabel dependen. Kemampuan mengukur pengaruh ini memungkinkan regresi untuk memprediksikan suatu hasil. Hal ini juga yang membuat variabel independen tak jarang disebut sebagai variabel prediktor dan variabel dependen disebut variabel outcome atau hasil. Mengenal regresi.

Pro Tips

• Uji korelasi adalah tes yang digunakan untuk mengukur kekuatan hubungan antar variabel.
• Jika kita ingin menguji korelasi dari dua variabel kategori, jenis tes yang kita gunakan adalah chi-square.
• Jika dua variabel yang ingin kita uji korelasinya berbentuk numerik, maka kita jenis tes yang dapat kita gunakan adalah korelasi koefisien.
• Korelasi tidak menjelaskan pengaruh karena tidak ada penjelasan mana variabel yang independen dan mana yang dependen.