Menguji Hipotesis
Melalui kelas ini, kamu diajak untuk:
- Mengenal probabilitas hasil p-value yang variatif dalam menguji hipotesis.
- Mengenal kekuatan uji statistik untuk mencegah kesalahan keputusan menolak atau menerima hipotesis.
Pengantar
Bayangkan kita tengah berada di pengadilan dan menunggu keputusan akhir. Sang juri, yang dalam konteks ini adalah p-value, dengan lantang menyatakan bahwa hipotesis nol gagal ditolak. Dengan wajah murung, kita pulang dan meratapi kegagalan dalam membuktikan hipotesis alternatif.

Menolak menyerah, kita mengajukan banding beberapa hari kemudian. Kali ini, untuk membuktikan hipotesis kita, sampel yang diambil lebih banyak dari sebelumnya. Setelah pengujian dilakukan, sang juri menyatakan bahwa hipotesis nol berhasil ditolak.
Mengulang Pengujian
Kasus di atas tak jarang ditemui dalam statistik. Saat kita menemukan p-value, bukan tak mungkin bahwa pengujian ulang dapat memberikan hasil berbeda. Dari kasus pengadilan di bagian sebelumnya, ditemukan bahwa putusan p-value > ambang batas p-value, katakan 0.05. Namun setelah pengujian ulang dengan sampel yang lebih besar, kita mendapatkan hasil p-value < 0.05.
P-Value adalah Probabilitas
Di kelas pengantar statistik, kita telah sedikit mengulas perihal p-value. P-value adalah probabilitas kebenaran dari hipotesis nol. Semakin tinggi p-value, semakin tinggi pula kemungkinan bahwa hipotesis nol adalah benar. Namun pada akhirnya, p-value mengukur probabilitas, bukan hasil pasti.
Misal kita menguji signifikansi perbedaan dengan menggunakan t-test. Pada pengujian pertama, kita mendapatkan p-value = 0.03. Tes kedua menggunakan sampel berbeda dan jumlah sama, kita mendapat p-value = 0.02. Pada tes ketiga, juga dengan sampel berbeda dan jumlah sama, p-value kembali menunjukkan angka 0.03. Namun pada tes ke-n, kita mungkin bisa mendapatkan hasil p-value = 0.06.
Melihat Data
Perhatikan perbedaan grafik di bawah ini.
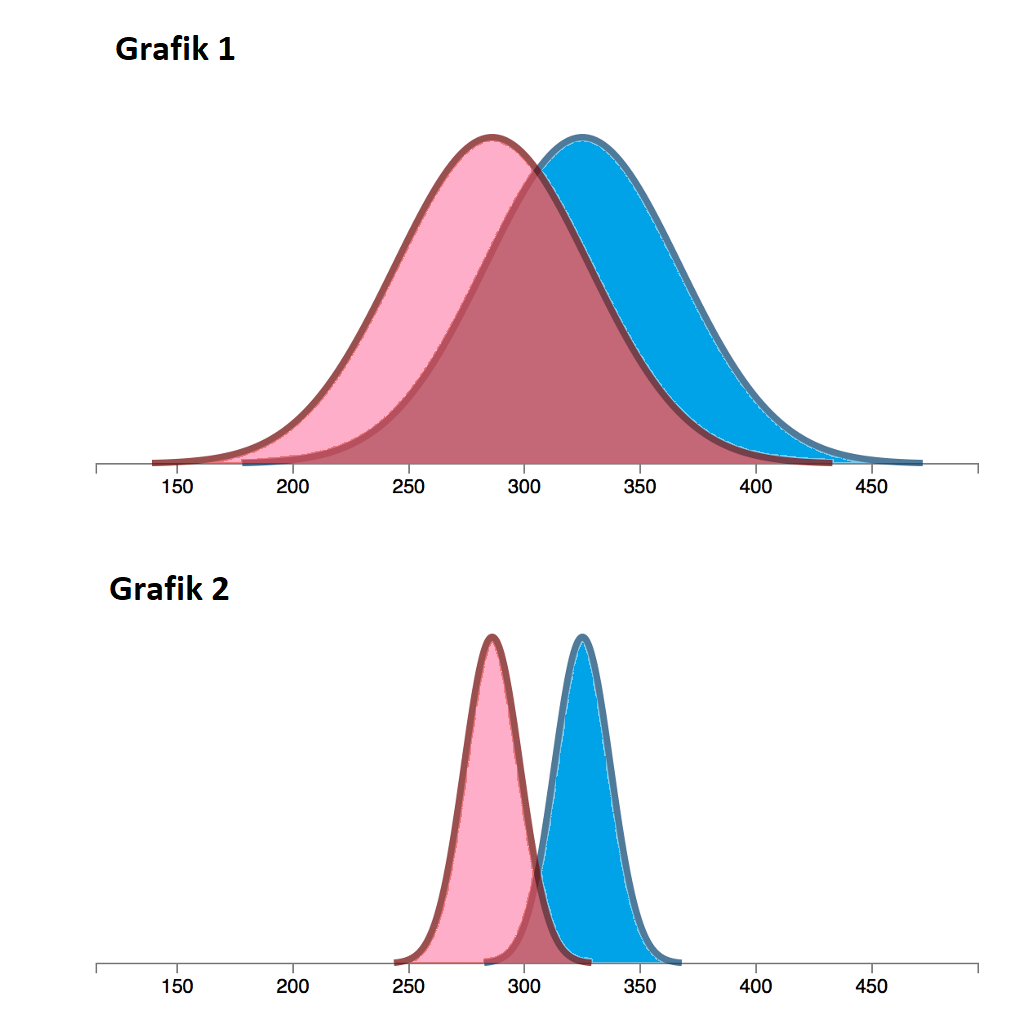
Di grafik pertama, ada overlap yang cukup besar antara data pertama dan data kedua. Sementara overlap data pertama dan kedua di grafik kedua. Meski data pertama (merah muda) dan kedua (biru) tampak berbeda di dua grafik tersebut, kita lebih mudah melihat perbedaan signifikan di grafik kedua.
Dengan kata lain, konsekuensi dari banyaknya overlap antar data adalah kemungkinan mendapatkan p-value yang tinggi. Namun, grafik pertama menunjukan ada perbedaan distribusi. Maka jika kita melakukan pengujian terus-menerus, ada kemungkinan kita mendapatkan p-value rendah.
Lalu, bagaimana cara untuk benar-benar yakin dengan p-value kita?
Kekuatan Uji Statistik
Dalam statistik, semua adalah soal probabilitas. Untuk benar-benar yakin bahwa p-value mampu dijadikan dasar untuk menolak hipotesis nol, kita perlu melihat kekuatan uji statistik. Jika p-value adalah probabilitas bahwa hipotesis nol adalah benar, kekuatan uji statistik adalah probabilitas kita mendapatkan p-value kecil. Dengan kata lain, kekuatan uji statistik adalah probabilitas kebenaran kita dalam menolak hipotesis nol.
Mari lihat kembali dua grafik yang telah kita singgung.

Dari kedua grafik ini, kemungkinan mendapatkan p-value kecil (ada perbedaan signifikan antara dua data) lebih besar untuk pengujian di grafik kedua ketimbang grafik pertama. Dengan demikian, semakin sedikit overlap antara dua data, semakin besar kekuatan uji statistiknya.
Pro Tips
- P-value adalah probabilitas sehingga dapat berubah-ubah ketika dilakukan pengujian ulang dengan jumlah sampel sama namun sampelnya berbeda.
- Variasi hasil p-value bermacam-macam, ada yang angkanya berubah tidak signifikan dan angkanya berubah secara signifikan (dari p-value < 0.05 menjadi > 0.05 atau sebaliknya).
- Probabilitas hasil p-value yang tetap kecil meski dilakukan pengujian berulang-ulang dinamakan kekuatan statistik.
Kuis
Dari dua data populasi, terdapat banyak overlap antara keduanya. Apa kecenderungan p-value yang dihasilkan oleh pengujian signifikansi perbedaan data tersebut?